Abstract
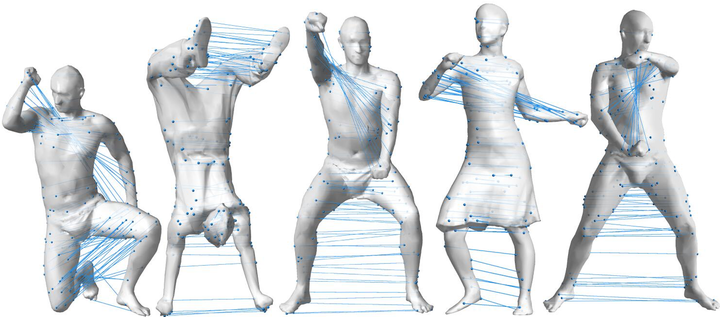
Reflectional symmetry is a ubiquitous pattern in nature. Previous works usually solve this problem by voting or sampling, suffering from high computational cost and randomness. In this paper, we propose a learning-based approach to intrinsic reflectional symmetry detection. Instead of directly finding symmetric point pairs, we parametrize this self-isometry using a functional map matrix, which can be easily computed given the signs of Laplacian eigenfunctions under the symmetric mapping. Therefore, we manually label the eigenfunction signs for a variety of shapes and train a novel neural network to predict the sign of each eigenfunction under symmetry. Our network aims at learning the global property of functions and consequently converts the problem defined on the manifold to the functional domain. By disentangling the prediction of the matrix into separated bases, our method generalizes well to new shapes and is invariant under perturbation of eigenfunctions. Through extensive experiments, we demonstrate the robustness of our method in challenging cases, including different topology and incomplete shapes with holes. By avoiding random sampling, our learning-based algorithm is over 20 times faster than state-of-the-art methods, and meanwhile, is more robust, achieving higher correspondence accuracy in commonly used metrics.
Supplementary notes can be added here, including code, math, and images.