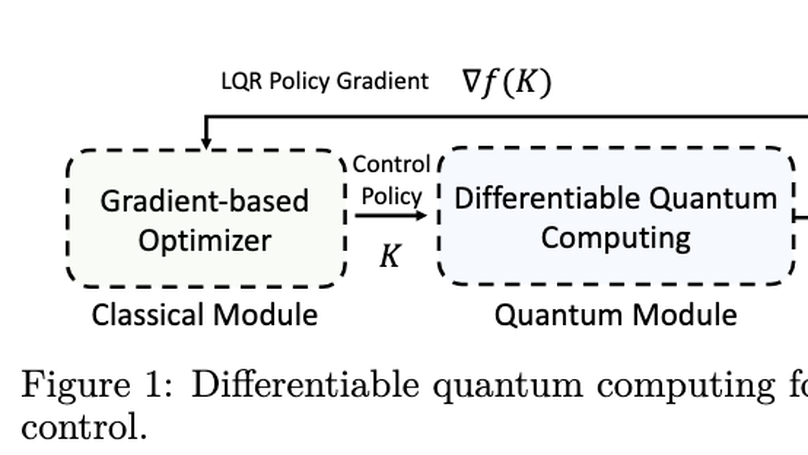
As industrial models and designs grow increasingly complex, the demand for optimal control of large-scale dynamical systems has significantly increased. However, traditional methods for optimal control incur significant overhead as problem dimensions grow. In this paper, we introduce an end-to-end quantum algorithm for linear-quadratic control with provable speedups. Our algorithm, based on a policy gradient method, incorporates a novel quantum subroutine for solving the matrix Lyapunov equation. Specifically, we build a quantum-assisted differentiable simulator for efficient gradient estimation that is more accurate and robust than classical methods relying on stochastic approximation. Compared to the classical approaches, our method achieves a super-quadratic speedup. To the best of our knowledge, this is the first end-to-end quantum application to linear control problems with provable quantum advantage.

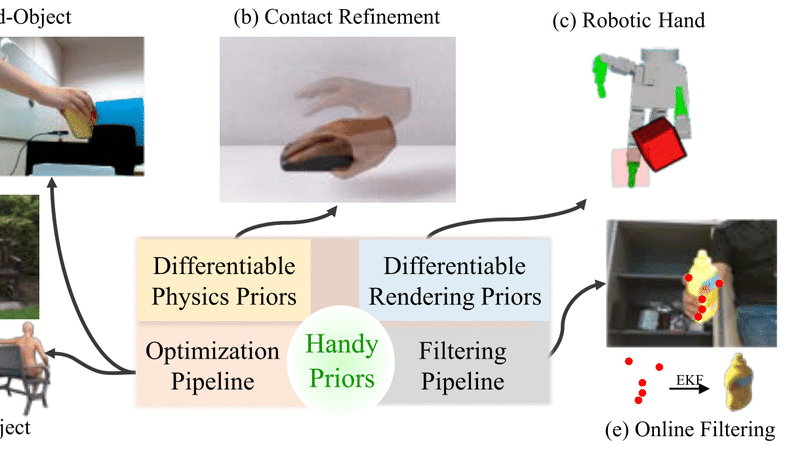
Various heuristic objectives for modeling hand-object interaction have been proposed in past work. However, due to the lack of a cohesive framework, these objectives often possess a narrow scope of applicability and are limited by their efficiency or accuracy. In this paper, we propose HandyPriors, a unified and general pipeline for pose estimation in human-object interaction scenes by leveraging recent advances in differentiable physics and rendering. Our approach employs rendering priors to align with input images and segmentation masks along with physics priors to mitigate penetration and relative-sliding across frames. Furthermore, we present two alternatives for hand and object pose estimation. The optimization-based pose estimation achieves higher accuracy, while the filtering-based tracking, which utilizes the differentiable priors as dynamics and observation models, executes faster. We demonstrate that HandyPriors attains comparable or superior results in the pose estimation task, and that the differentiable physics module can predict contact information for pose refinement. We also show that our approach generalizes to perception tasks, including robotic hand manipulation and human-object pose estimation in the wild.

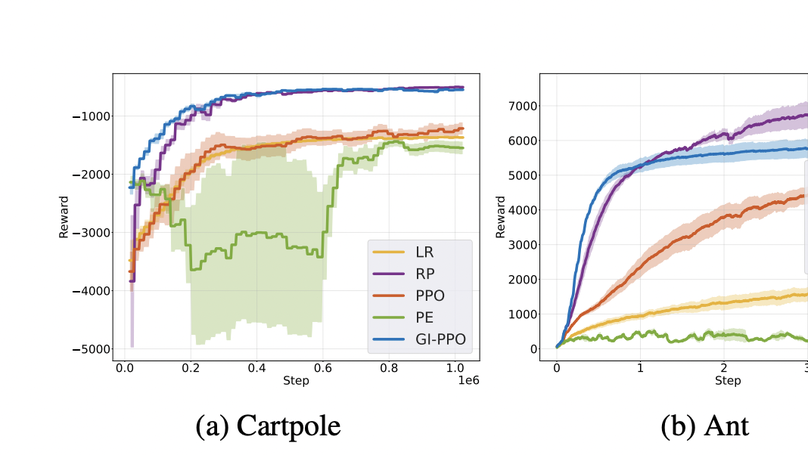
We introduce a novel policy learning method that integrates analytical gradients from differentiable environments with the Proximal Policy Optimization (PPO) algorithm. To incorporate analytical gradients into the PPO framework, we introduce the concept of an α-policy that stands as a locally superior policy. By adaptively modifying the α value, we can effectively manage the influence of analytical policy gradients during learning. To this end, we suggest metrics for assessing the variance and bias of analytical gradients, reducing dependence on these gradients when high variance or bias is detected. Our proposed approach outperforms baseline algorithms in various scenarios, such as function optimization, physics simulations, and traffic control environments. Our code can be found

We have witnessed very impressive progress in large-scale and multi-modal foundation/generative models in recent months. We believe making use of such models in a reasonable way could really enable robots to acquire diverse skills. In the recent white paper, we discussed how we can automate the whole pipeline for robotic skill learning, from low-level asset generation, texture generation, to high-level scene, task and reward generation. Once we obtain such a diverse suite of tasks and environments, we can offload policy training to RL of trajectory optimization to solve all the generated low-level tasks, and finally distill all the learned closed-loop policy into a unified policy model. Apart from scaling up in simulation, how to use real-world data more effectively is another promising research direction. Real-world human demonstrations can be found at scale, but typically only provides spatial trajectory information and doesn’t advise how to recover from error compounding during policy rollout. Motivated by these observations and thoughts, this workshop seeks to discuss and compare the advantages and limitations of different paradigms for scaling up skill learning - scaling up simulation, leveraging generative models, exploiting unstructured passive human demonstration, scaling up structured demonstration collection in the real world, etc.

Embedding polygonal mesh assets within photorealistic Neural Radience Fields (NeRF) volumes, such that they can be rendered and their dynamics simulated in a physically consistent manner with the NeRF, is under-explored from the system perspective of integrating NeRF into the traditional graphics pipeline. This paper designs a two-way coupling between mesh and NeRF during rendering and simulation. We first review the light transport equations for both mesh and NeRF, then distill them into a straightforward algorithm for updating radiance and throughput along a cast ray with an arbitrary number of bounces. To resolve the discrepancy between the linear color space that the path tracer assumes, versus the sRGB color space that standard NeRF uses, we train NeRF with High Dynamic Range (HDR) images. We also present a strategy to estimate light sources and cast shadows on the NeRF. Finally, we consider how the hybrid surface-volumetric formulation can be efficiently integrated with a high-performance physics simulator that supports cloth, rigid and soft bodies. The full rendering and simulation system can be run on a GPU at interactive rates. We show that a hybrid system approach outperforms alternatives in visual realism for mesh insertion, because it allows realistic light transport from volumetric NeRF media onto surfaces, which affects the appearance of reflective/refractive surfaces and illumination of diffuse surfaces informed by the scene.

Existing approaches to system identification (estimating the physical parameters of an object) from videos assume known object geometries. This precludes their applicability in a vast majority of scenes where object geometries are complex or unknown. In this work, we aim to identify parameters characterizing a physical system from a set of multi-view videos without any assumption on object geometry or topology. To this end, we propose “Physics Augmented Continuum Neural Radiance Fields” (PAC-NeRF), to estimate both the unknown geometry and physical parameters of highly dynamic objects from multi-view videos. We design PAC-NeRF to only ever produce physically plausible states by enforcing the neural radiance field to follow the conservation laws of continuum mechanics. For this, we design a hybrid Eulerian-Lagrangian representation of the neural radiance field, i.e., we use the Eulerian grid representation for NeRF density and color fields, while advecting the neural radiance fields via Lagrangian particles. This hybrid Eulerian-Lagrangian representation seamlessly blends efficient neural rendering with the material point method (MPM) for robust differentiable physics simulation. We validate the effectiveness of our proposed framework on geometry and physical parameter estimation over a vast range of materials, including elastic bodies, plasticine, sand, Newtonian and non-Newtonian fluids, and demonstrate significant performance gain on most tasks.

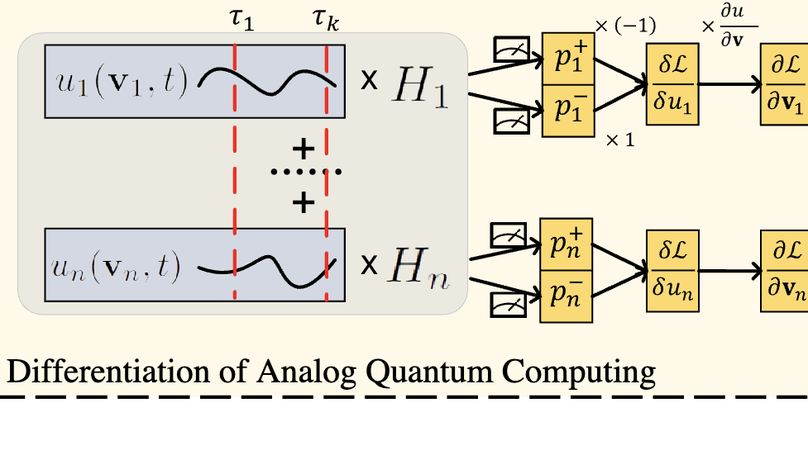
We formulate the first differentiable analog quantum computing framework with specific parameterization design at the analog signal (pulse) level to better exploit near-term quantum devices via variational methods. We further propose a scalable approach to estimate the gradients of quantum dynamics using a forward pass with Monte Carlo sampling, which leads to a quantum stochastic gradient descent algorithm for scalable gradient-based training in our framework. Applying our framework to quantum optimization and control, we observe a significant advantage of differentiable analog quantum computing against SOTAs based on parameterized digital quantum circuits by orders of magnitude.

We present a method for learning geometry and physics parameters of a dynamic scene requiring only a monocular RGB video. Our approach uses a hybrid representation of neural fields and hexahedra mesh, enabling objects in the scene to be interactively edited, and synthesized from novel views. To decouple the learning of underlying scene geometry from dynamic motion, we learn a time-invariant signed distance function which serves as a reference frame, as well as an associated deformation field that is conditioned on each time step. We design a two-way conversion between the neural field and corresponding mesh representation, which allows us to bridge the neural representation with a differentiable physics simulator, and therefore estimate physics parameters from the source video, by minimizing a cycle consistency loss. This flexible, hybrid representation also allows a user to easily edit 3D objects from the source video by directly editing the recovered hexahedra mesh, and propagating this operation back to the neural field. In Experiments, our method achieves higher-quality mesh and video reconstruction of dynamic scenes compared to other competitive Neural Field methods. Finally, we provide extensive examples which demonstrate our method’s ability to extract useful 3D representations of dynamic scenes from videos captured with consumer-grade cameras.

We introduce a novel differentiable hybrid traffic simulator, which simulates traffic using a hybrid model of both macroscopic and microscopic models and can be directly integrated into a neural network for traffic control and flow optimization. This is the first differentiable traffic simulator for macroscopic and hybrid models that can compute gradients for traffic states across time steps and inhomogeneous lanes. To compute the gradient flow between two types of traffic models in a hybrid framework, we present a novel intermediate conversion component that bridges the lanes in a differentiable manner as well. We also show that we can use analytical gradients to accelerate the overall process and enhance scalability. Thanks to these gradients, our simulator can provide more efficient and scalable solutions for complex learning and control problems posed in the traffic engineering than other existing algorithms.

We present a method for differentiable simulation of soft articulated bodies. Our work enables the integration of differentiable physical dynamics into gradient-based pipelines. We develop a top-down matrix assembly algorithm within Projective Dynamics and derive a generalized dry friction model for soft continuum using a new matrix splitting strategy. We derive a differentiable control framework for soft articulated bodies driven by muscles, joint torques, or pneumatic tubes. The experiments demonstrate that our designs make soft body simulation more stable and realistic compared to other frameworks. Our method accelerates the solution of system identification problems by more than an order of magnitude, and enables efficient gradient-based learning of motion control with soft robots.

We present a method for efficient differentiable simulation of articulated bodies. This enables integration of articulated body dynamics into deep learning frameworks, and gradient-based optimization of neural networks that operate on articulated bodies. We derive the gradients of the forward dynamics using spatial algebra and the adjoint method. Our approach is an order of magnitude faster than autodiff tools. By only saving the initial states throughout the simulation process, our method reduces memory requirements by two orders of magnitude. We demonstrate the utility of efficient differentiable dynamics for articulated bodies in a variety of applications. We show that reinforcement learning with articulated systems can be accelerated using gradients provided by our method. In applications to control and inverse problems, gradient-based optimization enabled by our work accelerates convergence by more than an order of magnitude.

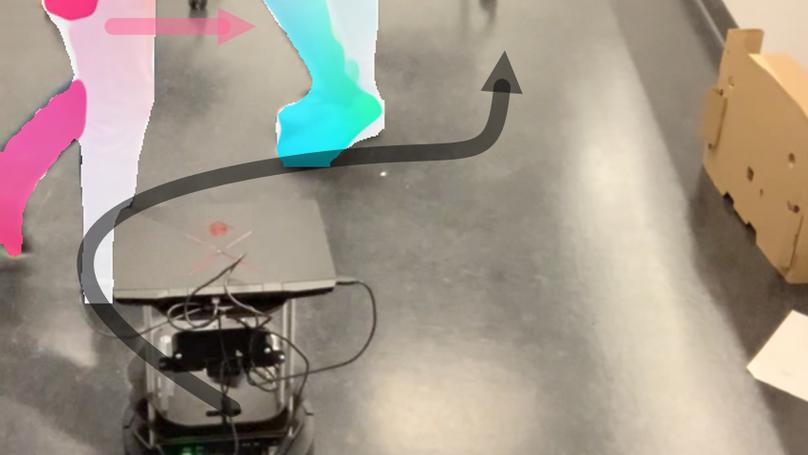
We present a modified velocity-obstacle (VO) algorithm that uses probabilistic partial observations of the environment to compute velocities and navigate a robot to a target. Our system uses commodity visual sensors, including a mono-camera and a 2D Lidar, to explicitly predict the velocities and positions of surrounding obstacles through optical flow estimation, object detection, and sensor fusion. A key aspect of our work is coupling the perception (OF, optical flow) and planning (VO) components for reliable navigation. Overall, our OF-VO algorithm using learning-based perception and model-based planning methods offers better performance than prior algorithms in terms of navigation time and success rate of collision avoidance. Our method also provides bounds on the probabilistic collision avoidance algorithm. We highlight the realtime performance of OF-VO on a Turtlebot navigating among pedestrians in both simulated and real-world scenes.

We introduce an efficient differentiable fluid simulator that can be integrated with deep neural networks as a part of layers for learning dynamics and solving control problems. It offers the capability to handle one-way coupling of fluids with rigid objects using a variational principle that naturally enforces necessary boundary conditions at the fluid-solid interface with sub-grid details. This simulator utilizes the adjoint method to efficiently compute the gradient for multiple time steps of fluid simulation with user defined objective functions. We demonstrate the effectiveness of our method for solving inverse and control problems on fluids with one-way coupled solids. Our method outperforms the previous gradient computations, state-of-the-art derivative-free optimization, and model-free reinforcement learning techniques by at least one order of magnitude.

Differentiable physics is a powerful approach to learning and control problems that involve physical objects and environments. While notable progress has been made, the capabilities of differentiable physics solvers remain limited. We develop a scalable framework for differentiable physics that can support a large number of objects and their interactions. To accommodate objects with arbitrary geometry and topology, we adopt meshes as our representation and leverage the sparsity of contacts for scalable differentiable collision handling. Collisions are resolved in localized regions to minimize the number of optimization variables even when the number of simulated objects is high. We further accelerate implicit differentiation of optimization with nonlinear constraints. Experiments demonstrate that the presented framework requires up to two orders of magnitude less memory and computation in comparison to recent particle-based methods. We further validate the approach on inverse problems and control scenarios, where it outperforms derivative-free and model-free baselines by at least an order of magnitude.

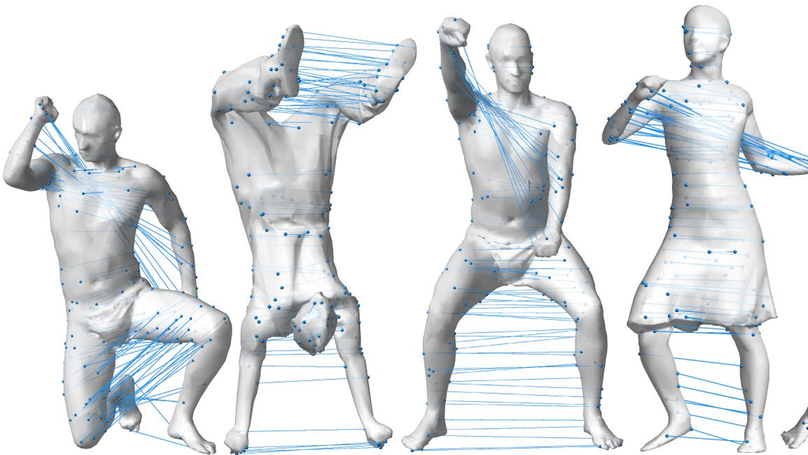
Reflectional symmetry is a ubiquitous pattern in nature. Previous works usually solve this problem by voting or sampling, suffering from high computational cost and randomness. In this paper, we propose a learning-based approach to intrinsic reflectional symmetry detection. Instead of directly finding symmetric point pairs, we parametrize this self-isometry using a functional map matrix, which can be easily computed given the signs of Laplacian eigenfunctions under the symmetric mapping. Therefore, we manually label the eigenfunction signs for a variety of shapes and train a novel neural network to predict the sign of each eigenfunction under symmetry. Our network aims at learning the global property of functions and consequently converts the problem defined on the manifold to the functional domain. By disentangling the prediction of the matrix into separated bases, our method generalizes well to new shapes and is invariant under perturbation of eigenfunctions. Through extensive experiments, we demonstrate the robustness of our method in challenging cases, including different topology and incomplete shapes with holes. By avoiding random sampling, our learning-based algorithm is over 20 times faster than state-of-the-art methods, and meanwhile, is more robust, achieving higher correspondence accuracy in commonly used metrics.

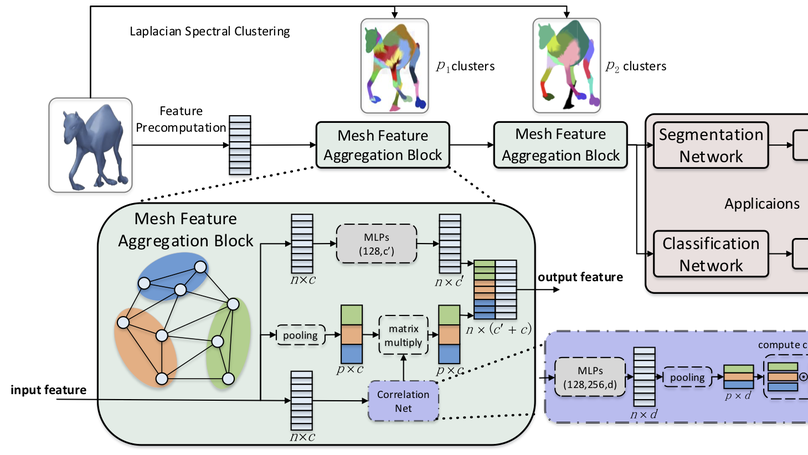
3D models are commonly used in computer vision and graphics. With the wider availability of mesh data, an efficient and intrinsic deep learning approach to processing 3D meshes is in great need. Unlike images, 3D meshes have irregular connectivity, requiring careful design to capture relations in the data. To utilize the topology information while staying robust under different triangulations, we propose to encode mesh connectivity using Laplacian spectral analysis, along with mesh feature aggregation blocks (MFABs) that can split the surface domain into local pooling patches and aggregate global information amongst them. We build a mesh hierarchy from fine to coarse using Laplacian spectral clustering, which is flexible under isometric transformations. Inside the MFABs there are pooling layers to collect local information and multi-layer perceptrons to compute vertex features of increasing complexity. To obtain the relationships among different clusters, we introduce a Correlation Net to compute a correlation matrix, which can aggregate the features globally by matrix multiplication with cluster features. Our network architecture is flexible enough to be used on meshes with different numbers of vertices. We conduct several experiments including shape segmentation and classification, and our method outperforms state-of-the-art algorithms for these tasks on the ShapeNet and COSEG datasets.

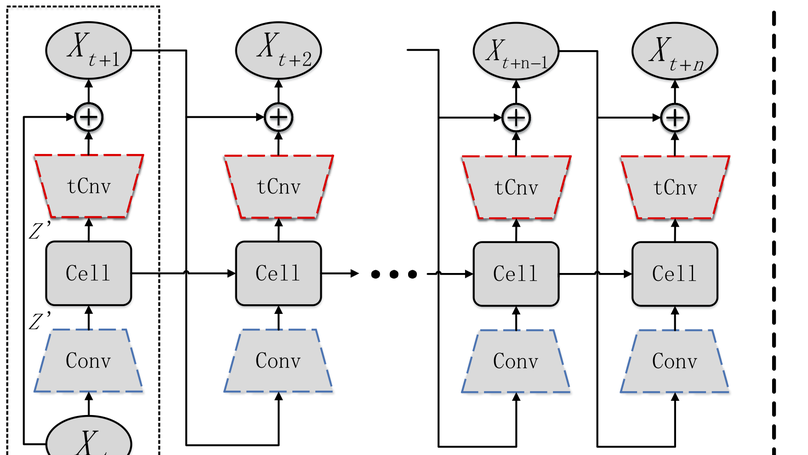
Synthesizing realistic 3D mesh deformation sequences is a challenging but important task in computer animation. To achieve this, researchers have long been focusing on shape analysis to develop new interpolation and extrapolation techniques. However, such techniques have limited learning capabilities and therefore often produce unrealistic deformation. Although there are already networks defined on individual meshes, deep architectures that operate directly on mesh sequences with temporal information remain unexplored due to the following major barriers, irregular mesh connectivity, rich temporal information, and varied deformation. To address these issues, we utilize convolutional neural networks defined on triangular meshes along with a shape deformation representation to extract useful features, followed by long short-term memory (LSTM) that iteratively processes the features. To fully respect the bidirectional nature of actions, we propose a new share-weight bidirectional scheme to better synthesize deformations. An extensive evaluation shows that our approach outperforms existing methods in sequence generation, both qualitatively and quantitatively.

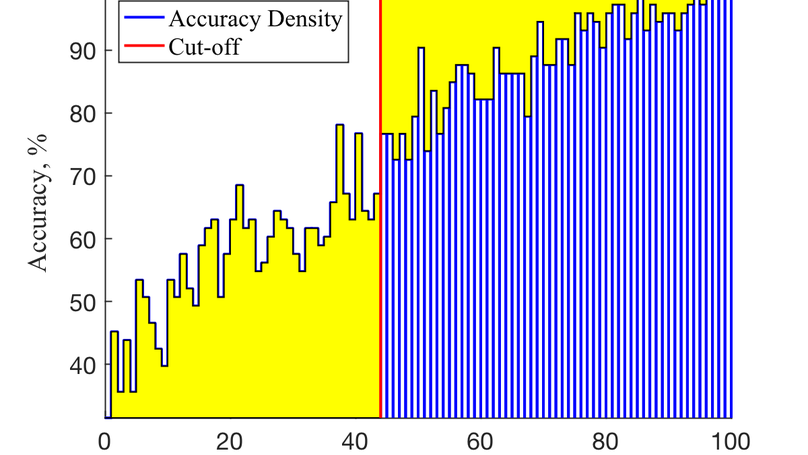
Semi-supervised learning uses underlying relationships indata with a scarcity of ground-truth labels. In this paper, we intro-duce an uncertainty quantification (UQ) method for graph-basedsemi-supervised multi-class classification problems. We not onlypredict the class label for each data point, but also provide a con-fidence score for the prediction. We adopt a Bayesian approachand propose a graphical multi-class probit model together withan effective Gibbs sampling procedure. Furthermore, we proposea confidence measure for each data point that correlates with theclassification performance. We use the empirical properties ofthe proposed confidence measure to guide the design of a human-in-the-loop system. The uncertainty quantification algorithm andthe human-in-the-loop system are successfully applied to classifi-cation problems in image processing and ego-motion analysis ofbody-worn videos

Transferring deformation from a source shape to a target shape is a very useful technique in computer graphics. State-of-the-art deformation transfer methods require either point-wise correspondences between source and target shapes, or pairs of deformed source and target shapes with corresponding deformations. However, in most cases, such correspondences are not available and cannot be reliably established using an automatic algorithm. Therefore, substantial user effort is needed to label the correspondences or to obtain and specify such shape sets. In this work, we propose a novel approach to automatic deformation transfer between two unpaired shape sets without correspondences. 3D deformation is represented in a highdimensional space. To obtain a more compact and effective representation, two convolutional variational autoencoders are learned to encode source and target shapes to their latent spaces. We exploit a Generative Adversarial Network (GAN) to map deformed source shapes to deformed target shapes, both in the latent spaces, which ensures the obtained shapes from the mapping are indistinguishable from the target shapes. This is still an under-constrained problem, so we further utilize a reverse mapping from target shapes to source shapes and incorporate cycle consistency loss, i.e. applying both mappings should reverse to the input shape. This VAE-Cycle GAN (VC-GAN) architecture is used to build a reliable mapping between shape spaces. Finally, a similarity constraint is employed to ensure the mapping is consistent with visual similarity, achieved by learning a similarity neural network that takes the embedding vectors from the source and target latent spaces and predicts the light field distance between the corresponding shapes. Experimental results show that our fully automatic method is able to obtain high-quality deformation transfer results with unpaired data sets, comparable or better than existing methods where strict correspondences are required.

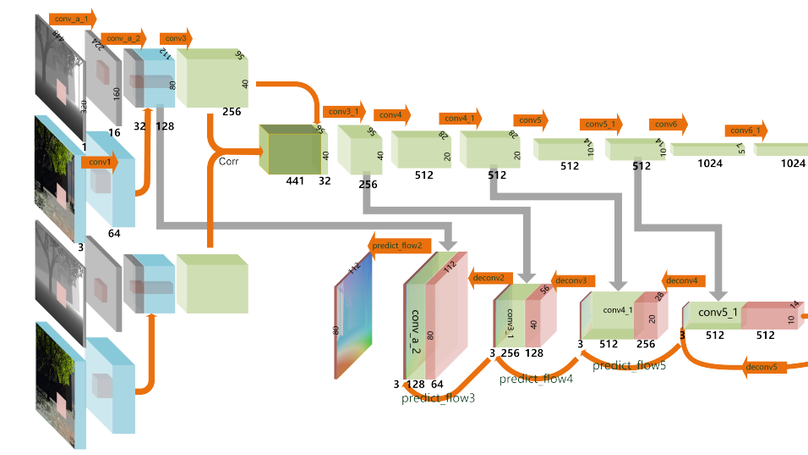
With the rapid development of depth sensors, RGB-D data has become much more accessible. Scene flow is one of the fundamental ways to understand the dynamic content in RGB-D image sequences. Traditional approaches estimate scene flow using registration and smoothness or local rigidity priors, which is slow and prone to errors when the priors are not fully satisfied. To address such challenges, learning based methods provide an attractive alternative. However, trivially applying CNN-based optical flow estimation methods does not produce satisfactory results. How to use deep learning to improve the estimation of scene flow from RGB-D images remains unexplored. In this work, we propose a novel learning based framework to estimate scene flow, which takes both brightness and scene flow losses. Given a pair of RGB-D images, the brightness loss is used to measure the disparity between the first RGB-D image and the deformed second RGB-D image using the scene flow, and the scene flow loss is used to learn from the ground truth of scene flow. We build a convolutional neural network to simultaneously optimize both losses. Extensive experiments on both synthetic and real-world datasets show that our method is significantly faster than existing methods and outperforms stateof-the-art real-time methods in accuracy.